Implementation of WorldQuant Alphas, Meta Strategies
Published at Mar 17, 2024
OpenMP Performance
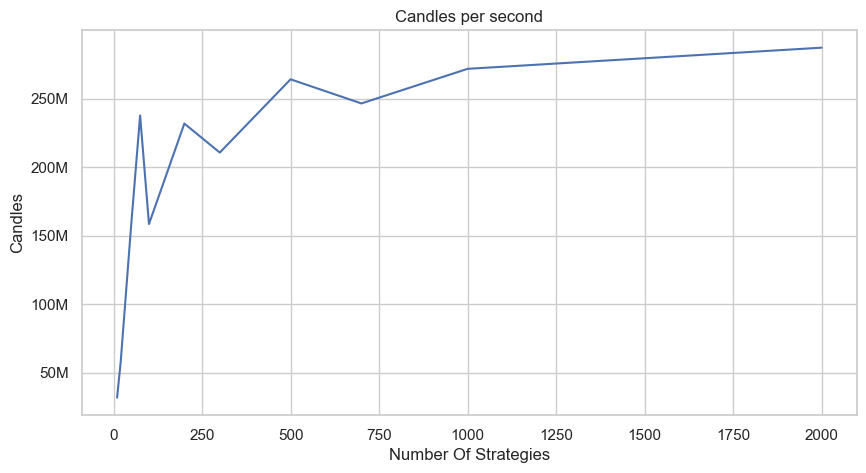
Table of Contents
Intro
In my previous post I looked and introducing volatility scaling and targeting, some grid search work for hyper parameter tuning, as well as some visual work on the GUI. In this one I wanted to cover some inhacements to the abstract strategy tree so you can express more complex strategies without compromising on performance. To do this, I took some inspiration from WorldQuant’s idea of “Alphas”, or small composible and formulaic strategies designed to be applied over large asset universes. The idea being you create a set of alpha signals with hopefully low correlation to each other and combine them to create a portfolio. For more info check out: https://arxiv.org/ftp/arxiv/papers/1601/1601.00991.pdf
This kind of strategy is well suited to the vectorized approach of Atlas, so I wanted to implement them. I have made quite a view changes over the past month, but here I highlight the introduction of observers, models, and meta strategies going into depth below. As a refresher, Atlas is a high performance Algorthmic Trading Backtesting library written in C++23 with a Python wrapper build using pybind11. To get a better sense you can check out historical posts, though I admit some of the code as been refactored (work in progress)
Asset Observers
To start look at Alpha#2:(-1 * correlation(rank(delta(log(volume), 2)), rank(((close - open) / open)), 6)). It is made up of smaller functions designed to be applied over a rolling basis on a per asset level. To calculate this you need the 2 period change in log volumn and the (close-open)/open. You then rank these two features and then look at the 6 period correlation, then scale positioning according to the inverse of that. Most of these alphas are most likely the result of some optimization or search process, but it is interesting to look at and tricky to implement.
To do this we define a new class called AssetObserverNode. This class is responsible for maintaining a rolling buffer of data over every asset and applying some function over it, we start with the abstract class
//============================================================================
export class AssetObserverNode
: public StrategyBufferOpNode
{
private:
/// <summary>
/// Rolling window size of observation
/// </summary>
size_t m_window = 0;
/// <summary>
/// Buffer matrix holding previous observations of the observer.
/// </summary>
LinAlg::EigenMatrixXd m_buffer_matrix;
/// <summary>
/// Current index into the buffer to write to. On cacheObserver, the m_buffer_idx - 1
/// column is overwritten with the new observation. Then onOutOfRange is called on m_buffer_idx
/// to update the observer with the column that is about to be overwritten in the next step
/// </summary>
size_t m_buffer_idx = 0;
protected:
LinAlg::EigenVectorXd m_signal;
LinAlg::EigenVectorXd m_signal_copy;
public:
AssetObserverNode(
Option<String> name,
SharedPtr<StrategyBufferOpNode> parent,
AssetObserverType observer_type,
size_t window
) noexcept;
ATLAS_API virtual ~AssetObserverNode() noexcept;
SharedPtr<StrategyBufferOpNode> m_parent;
AssetObserverType m_observer_type;
[[nodiscard]] auto const& getBufferMatrix() const noexcept { return m_buffer_matrix; }
/// <summary>
/// On exchange step method is called to update the observer with the new observation
/// </summary>
void cacheBase() noexcept;
/// <summary>
/// Get a mutable ref into the observers buffer matrix at the current index
/// </summary>
/// <returns></returns>
LinAlg::EigenRef<LinAlg::EigenVectorXd> buffer() noexcept;
/// <summary>
/// Called when column is out of range from the rolling window
/// </summary>
/// <param name="buffer_old"></param>
virtual void onOutOfRange(LinAlg::EigenRef<LinAlg::EigenVectorXd> buffer_old) noexcept = 0;
/// <summary>
/// Pure virtual method defining the observer's evaluation method
/// </summary>
virtual void cacheObserver() noexcept = 0;
/// <summary>
/// Actual evaluation of the observer, copies the signal buffer into the target. Optionally allows
/// override if observer is a managed view of another observer.
/// </summary>
/// <param name="target"></param>
virtual void evaluate(LinAlg::EigenRef<LinAlg::EigenVectorXd> target) noexcept;
};The base class is responsible for mainting a rolling window of data and it does so by holding and Eigen Matrix of historical values and using a circular index to maintain the position into the buffer. Every step forward in time cahceBase() is called exactly once to generate the signal at the time. This way strategies can share observers without having to recompute.
Essentially at every time step t1, we evaluate the parent, this could be something like taking (close - open) / open as we saw in the example above. We then apply the observer to this, such as taking the n period change. After that, we copy this signal over and handle the column going out of bounds.
//============================================================================
void AssetObserverNode::cacheBase() noexcept {
if (m_exchange.currentIdx() < m_observer_warmup) {
return;
}
// evaluate the parent function onto the buffer
auto buffer_ref = buffer();
m_parent->evaluate(buffer_ref);
// apply derived class implementation of observeration
cacheObserver();
// copy the column into the cache if needed
if (hasCache() && m_exchange.currentIdx() >= (m_window - 1))
cacheColumn() = m_signal;
// when a column is about to go out of range update and call
// derived class to handle it.
m_buffer_idx = (m_buffer_idx + 1) % m_window;
m_signal_copy = m_signal;
if (m_exchange.currentIdx() >= (m_window - 1))
onOutOfRange(m_buffer_matrix.col(m_buffer_idx));
}Looking now at a concrete implementation, we look at the MaxObserverNode which tracks the relative index of the maximum value in the window, i.e. [2,8,2,1] -> 8 and [2,5,4,6] -> 6. The cacheObserver function is fairly straight forward using eigen, just take take the component wise max compared to the what already have in the buffer, taking advtange of the fact the buffer holds the current max.
//============================================================================
void MaxObserverNode::cacheObserver() noexcept {
m_signal = buffer().cwiseMax(m_signal);
}The hard part comes when the value that is the current max is going out of range of the window. If the window is [8,2,4,1] then the new max will become 4. To implement this we loop over the rows of the buffer matrix (each representing a window into the asset) and observer if the value going out of range is the max value. If that is the case, we need to loop over the row to find the new max.
//============================================================================
void MaxObserverNode::onOutOfRange(
LinAlg::EigenRef<LinAlg::EigenVectorXd> buffer_old) noexcept {
assert(buffer_old.size() == m_signal.size());
size_t buffer_idx = getBufferIdx();
auto const &buffer_matrix = getBufferMatrix();
for (size_t i = 0; i < static_cast<size_t>(m_signal.rows()); i++) {
// Check if the column going out of range holds the max value for the row
if (buffer_old(i) != m_signal(i)) {
continue;
}
// loop over the buffer row and find the new max, skipping the expiring
// index
size_t columns = static_cast<size_t>(buffer_matrix.cols());
double max = -std::numeric_limits<double>::max();
for (size_t j = 0; j < columns; j++) {
if (buffer_matrix(i, j) > max && j != buffer_idx) {
max = buffer_matrix(i, j);
}
}
m_signal(i) = max;
}
}There is most likely some room for some optimization and more aggresive use of eigen’s built in functions, but this works and helps us track the max value over a sliding window for every asset listed at the same time. A trickier question is maintaining the index of the mas value. Due to the fact we are using a rotating buffer the current index into the buffer can not be used as the zero index for the window. For example, the buffer might hold [3,2,1,4] and you thing the arg max is 4, but the last element could be the start of the sliding window, i.e. the actual window is [4,3,2,1] in which case the arg max is 1.
To look at this we use TsArgMaxObserverNode which does just that. It holds a max observer and watches as the max is about to go out of the window to update. The cacheObserver is a little harder, essentially it grabs the max observers buffer matrix and grabs its signal copy. If the col at the buffer index is equal to the max signal, then then the arg max is V (i.e. the window size), otherwise it is 1 minus the previous value (i.e. the max didnt change but it is one more step into the past compared to previous)
//============================================================================
void TsArgMaxObserverNode::cacheObserver() noexcept {
auto const &buffer_matrix = m_max_observer->getBufferMatrix();
auto v = static_cast<double>(getWindow());
m_signal = (buffer_matrix.col(getBufferIdx()).array() ==
m_max_observer->getSignalCopy().array())
.select(v, m_signal.array() - 1);
}
If the max value is about to go out of range it becomes hard. We have to find the new max value and calculate it’s correct index relative to the true start of the window. Once you find the correct index, the reset is fairly straight forward, simply update the signal column in place.
void TsArgMaxObserverNode::onOutOfRange(
LinAlg::EigenRef<LinAlg::EigenVectorXd> buffer_old) noexcept {
size_t buffer_idx = getBufferIdx();
size_t window = getWindow();
auto const &buffer_matrix = m_max_observer->getBufferMatrix();
size_t columns = static_cast<size_t>(buffer_matrix.cols());
for (size_t i = 0; i < static_cast<size_t>(m_signal.rows()); i++) {
auto const &row = buffer_matrix.row(i);
// Column going out of range is the argmax if the value is equal to the
// window, otherwise it is not the argmax and we can skip it
auto old = m_signal(i);
if (old > 1) {
continue;
}
// get the max coefficient from the buffer row
double max = -std::numeric_limits<double>::max();
size_t max_idx = 0;
for (size_t j = 0; j < columns; j++) {
if (row(j) > max) {
max = row(j);
max_idx = j;
}
}
max_idx = (max_idx - buffer_idx + window) % window;
max_idx += 1;
m_signal(i) = static_cast<double>(max_idx);
cacheColumn()(i) = m_signal(i);
}
}These are perhaps the trickier onces, many are more straightforward and can build on top of each other. Additionally, many don’t require out of range calls. Below are some additional examples for clarity. For more info take a look at: https://github.com/ntorm1/Atlas/blob/main/modules/ast/ObserverNode.ixx
//============================================================================
void VarianceObserverNode::cacheObserver() noexcept {
m_mean_observer->evaluate(m_signal);
auto sum_squared_cache = m_sum_squared_observer->getSignalCopy();
m_signal =
sum_squared_cache - (getWindow() * m_signal.cwiseProduct(m_signal));
if (getWindow() > 1)
m_signal /= static_cast<double>(getWindow() - 1);
}
//============================================================================
void LinearDecayNode::cacheObserver() noexcept {
if (is_first_step) {
m_decay_buffer = buffer();
is_first_step = false;
} else {
m_decay_buffer = (1.0 - m_alpha) * m_decay_buffer + m_alpha * buffer();
}
}
//============================================================================
void CorrelationObserverNode::cacheObserver() noexcept {
auto const &left_variance_cache = m_left_var_observer->getSignalCopy();
auto const &right_variance_cache = m_right_var_observer->getSignalCopy();
auto const &covariance_cache = m_cov_observer->getSignalCopy();
m_signal = covariance_cache.cwiseQuotient(
(left_variance_cache.cwiseSqrt() * right_variance_cache.cwiseSqrt()));
}
Models
The above samples are all agnostic towards their input and can be stacked on top of each other, i.e. finding correlation between two ts arg max nodes and more. This will allow you build many of the world quant alphas, but some functions are missing and will hopefully be added in the coming days. Antother interesting addition is Models, the operate over a set of features (like the observer above) and train a model over some historical view in order to generate predictions which can be used as signals.
Again we start with the abstract base class for models. It mainly functions to provide helper utilities for managing views into historical data and for now is quite simple. Essentially we define some historical training window to use, and a walk forward window that defines the frequency in which to update.
//============================================================================
export class ModelConfig
{
public:
size_t training_window;
size_t walk_forward_window;
ModelType type;
SharedPtr<Exchange> exchange;
Option<ModelScalingType> scaling_type = std::nullopt;
ModelConfig() = delete;
ATLAS_API ModelConfig(
size_t training_window,
size_t walk_forward_window,
ModelType model_type,
SharedPtr<Exchange> exchange
) noexcept;
ATLAS_API ~ModelConfig() noexcept = default;
};
//============================================================================
export class ModelBase : public AST::StrategyBufferOpNode
{
friend class Exchange;
private:
ModelBaseImpl* m_impl;
SharedPtr<Exchange> m_exchange;
size_t m_buffer_idx = 0;
void stepBase() noexcept;
protected:
LinAlg::EigenMatrixXd m_X;
LinAlg::EigenVectorXd m_y;
LinAlg::EigenVectorXd m_signal;
SharedPtr<ModelConfig> m_config;
template <typename FloatType, typename EigenMatrixType, typename EigenVectorType>
void copyBlocks(
LinAlg::EigenRef<EigenMatrixType> x_train,
LinAlg::EigenRef<EigenVectorType> y_train
) const noexcept;
[[nodiscard]] LinAlg::EigenBlock getXPredictionBlock() const noexcept;
public:
ATLAS_API ModelBase(
String id,
Vector<SharedPtr<AST::StrategyBufferOpNode>> features,
SharedPtr<ModelTarget> target,
SharedPtr<ModelConfig> config
) noexcept;
ATLAS_API virtual ~ModelBase() noexcept;
void evaluate(LinAlg::EigenRef<LinAlg::EigenVectorXd> target) noexcept final override;
void step() noexcept;
virtual void train() noexcept = 0;
virtual void predict() noexcept = 0;
};We start with the step function. A model holds a vector of features, such as the asset observers we saw earlier ands is responsible for copying and maintaining a historical view into the data. Again we use a Eigen Matrix with a circular index, this does complicate things significantly but also reduces any copying of the data. Additionally, the model target is a future look into the future so indexing it is quite tricky. At time t1 we want to defined the target as the close at t3, we only know the result at t3. So the target is evaluated late and then shifted back to the correct index. Thus the step function is mostly responsible of mainting the Eigen blocks with the correct indexing.
//============================================================================
void ModelBase::step() noexcept {
auto const &features = getFeatures();
auto const &target = getTarget();
// check for buffer index loop around and reset to 0
if (m_buffer_idx == static_cast<size_t>(m_X.rows())) {
m_buffer_idx = 0;
m_buffer_looped = true;
}
// get the features x block starting at buffer index and number of rows
// equal to the number of assets. Evaluate the features directly into the
// block view, with constant being at the end of the block past features
assert(m_buffer_idx + m_asset_count <= static_cast<size_t>(m_X.rows()));
auto x_block = m_X.block(m_buffer_idx, 0, m_asset_count, features.size());
for (size_t i = 0; i < features.size(); ++i) {
features[i]->evaluate(x_block.col(i));
}
m_buffer_idx += m_asset_count;
// if past look forward copy the features target into the y block scaled back
// to where the corresponding features were evaluated
size_t look_forward = target->getLookForward();
if (getCurrentIdx() > look_forward) {
// if we haven't reached the end of the buffer size check to make sure the
// buffer idx is past the look forward window.
if (!m_buffer_looped)
assert(m_buffer_idx >= m_asset_count * (look_forward + 1));
// look to find the start of the y block for the corresponding featues. If
// the buffer recently looped around then we have to look at the end of the
// buffer and find the relative depth to the back of the buffer. Otherwise
// we can just look back from the current buffer index
size_t y_block_row_start;
if (m_asset_count * (look_forward + 1) > m_buffer_idx) {
size_t buffer_relative_index = m_buffer_idx / m_asset_count;
y_block_row_start = m_X.rows() - m_asset_count * (look_forward + 1 -
buffer_relative_index);
} else {
y_block_row_start = m_buffer_idx - m_asset_count * (look_forward + 1);
}
assert(y_block_row_start + m_asset_count <=
static_cast<size_t>(m_y.rows()));
auto y_block = m_y.block(y_block_row_start, 0, m_asset_count, 1);
target->evaluate(y_block);
}
}This function is called at every step and maintains the X and Y data for the model to use. Then, whenever the training window evenly divides the time index, the model is fit to the data. Hear we look at the linear regression implentation as it is the most striaght forward.
//============================================================================
void LinearRegressionModel::train() noexcept {
size_t look_forward = getTarget()->getLookForward();
size_t training_window = m_config->training_window;
LinAlg::EigenMatrixXd m_X_train(training_window - look_forward,
m_theta.size());
LinAlg::EigenVectorXd m_y_train(training_window - look_forward);
copyBlocks<double, LinAlg::EigenMatrixXd, LinAlg::EigenVectorXd>(m_X_train,
m_y_train);
if (m_lr_config->m_orthogonalize_features)
gramSchmidtOrthogonalization(m_X_train);
switch (m_lr_config->m_solver) {
case LinearRegressionSolver::LDLT:
m_theta = (m_X_train.transpose() * m_X_train)
.ldlt()
.solve(m_X_train.transpose() * m_y_train);
break;
case LinearRegressionSolver::ColPivHouseholderQR:
...
}
}The simplist and fastest ways uses simple formulas from linear algebra to solve the linear regression and is nothing to interesting. There are some other implementations like lasso regression, but leave the out for now. The main trick comes down to copy blocks. This builds the training set from the circular buffer which is hard for two reasons.
One, it uses relative indexing so we might have to copy from two different blocks. And two, the last #look_forward number of samples haven’t generate the target variable yet so they must be left out. You’ll notice it also is templated over the scaler type, xgboost for example likes float so template will cast to the appropriate type but we leave that out here.
//============================================================================
template <typename FloatType, typename EigenMatrixType,
typename EigenVectorType>
void ModelBase::copyBlocks(
LinAlg::EigenRef<EigenMatrixType> x_train,
LinAlg::EigenRef<EigenVectorType> y_train) const noexcept {
size_t look_forward = getTarget()->getLookForward();
size_t training_window = m_config->training_window;
size_t buffer_col_size = static_cast<size_t>(m_X.cols());
// if the buffer has looped around then we have to copy the features and
// target into the training blocks in two steps. First we copy the features
// and target from 0 to the buffer index for the newest features, then copy
// from the back starting at the end of the buffer offset by the number of
// rows remaining in the training window.
if (m_buffer_looped && m_buffer_idx >= m_asset_count * (look_forward + 1)) {
// get the end of front portion of buffer offset by the look forward window
size_t front_end_idx = m_buffer_idx - m_asset_count * (look_forward);
size_t remaining_rows =
training_window - (front_end_idx / m_asset_count) - look_forward;
size_t remaining_start = m_X.rows() - m_asset_count * remaining_rows;
x_train.block(0, 0, front_end_idx, buffer_col_size) =
m_X.block(0, 0, front_end_idx, buffer_col_size).cast<FloatType>();
y_train.block(0, 0, front_end_idx, 1) =
m_y.block(0, 0, front_end_idx, 1).cast<FloatType>();
x_train.block(front_end_idx, 0, remaining_rows, buffer_col_size) =
m_X.block(remaining_start, 0, remaining_rows, buffer_col_size)
.cast<FloatType>();
y_train.block(front_end_idx, 0, remaining_rows, 1) =
m_y.block(remaining_start, 0, remaining_rows, 1).cast<FloatType>();
m_y.block(remaining_start, 0, remaining_rows, 1);
}
} else {
// if buffer has wrapped around but it hasn't passed the look forward window
// then we can just copy the features from the back of the buffer offest by
// the difference between the look forward window and the buffer index
size_t train_end_idx;
if (m_buffer_looped) {
train_end_idx =
m_X.rows() -
m_asset_count * (look_forward - m_buffer_idx / m_asset_count);
} else {
train_end_idx = m_buffer_idx - m_asset_count * look_forward;
}
size_t train_start_idx =
train_end_idx - m_asset_count * (training_window - look_forward);
size_t train_block_size = train_end_idx - train_start_idx;
if constexpr (std::is_same_v<FloatType, float>) {
x_train = m_X.block(train_start_idx, 0, train_block_size, buffer_col_size)
.cast<FloatType>();
y_train =
m_y.block(train_start_idx, 0, train_block_size, 1).cast<FloatType>();
}
}
}The main head ache again comes from indexing, but once we copy the data over from the buffers the training is fairly straight forward as we saw above. Once the model training is complete, the predictions are generated every step and stored in a temp buffer. For linear regression that becomes quite straight forward.
Meta Strategies
Finally, we look at meta strategies, or strategies that don’t have any evaluation logic, but are simply the weighting of some set of child strategies. Building off the world quant example, you might have 10 alphas implemented, then you could make a composite strategy that applies some portfolio weighting to each to take advantage of uncorrelated returns. To do this I stripped out much of the strategy logic from the Strategy class you might see from my old posts into an abstract Allocator class. Now you have the MetaStrategy class the derives from that and holds the child strategies seen here in the private implementation.
//============================================================================
struct MetaStrategyImpl {
Vector<SharedPtr<Allocator>> child_strategies;
HashMap<String, size_t> strategy_map;
LinAlg::EigenMatrixXd weights;
LinAlg::EigenVectorXd child_strategy_weights;
LinAlg::EigenVectorXd meta_weights;
};
The weights matrix is an M by N matrix where M is the number of assets in the exchange and N is the number of strategies held by the meta class. child_strategy_weights is a size N vector holding the % allocation towards each child strategy held by the meta strategy. Finally meta_weights holds the actual weights of the meta class calculated from the children and updated at every step. Without rehashing a lot of the functonality and logic behind the strategy class as I have posted before, is the meta strategy update function called every time step.
//============================================================================
void MetaStrategy::step() noexcept {
if (!m_step_call || !m_impl->child_strategies.size()) {
return;
}
evaluate(m_impl->meta_weights);
#pragma omp parallel for
for (int i = 0; i < m_impl->child_strategies.size(); i++) {
auto target_weights = m_impl->weights.col(static_cast<int>(i));
auto &strategy = m_impl->child_strategies[i];
strategy->step(target_weights);
if (strategy->getIsMeta()) {
auto meta_strategy = static_cast<MetaStrategy *>(strategy.get());
meta_strategy->step();
}
}
step(m_impl->meta_weights);
}Each time step we evaluate over the current weights then we update the children. Note two things, Each of the child strategies are completley independant and the abstract strategy tree was designed to be thread safe and shared across strategies (including oberservers and models.) Thus we use OpenMP to loop over the child strategy vector in parralell and step all forward in time.
Second, child strategies can themselves be meta classes, so we have to check the type of each and recursively call the child step functions as needed. I have yet to test a deep multi level tree yet, but that is the idea.
Finally, after all the chld strategies have update, we need to update the meta strategies weights accordingly. For now we just get the weighted row wise mean of the weights matrix.
//============================================================================
void MetaStrategy::step(
LinAlg::EigenRef<LinAlg::EigenVectorXd> target_weights_buffer) noexcept {
// weights holds an M by N matrix of portfolio weights for the child
// strategies where M is the number of assets and N is the number of child
// strategies, to get the parent allocation, get the row-wise weighted mean
assert(m_impl->weights.cols() == m_impl->child_strategy_weights.rows());
assert(target_weights_buffer.rows() == m_impl->weights.rows());
target_weights_buffer = (m_impl->weights.array().rowwise() *
m_impl->child_strategy_weights.array().transpose())
.rowwise()
.sum();
m_step_call = false;
}Again taking advtange of Eigen, the above is extremly fast to do and scales to huge amounts of strategies. The next step would be to dynamically update the strategy weightings based on historical and predicted performance, correlation, and more to efficently allocate capital across a range of strategies. Mean reversion might to well in certain times, while momentum in others, etc.
With this inplace I went ahead and tested the speed of the implemetation with a very simple strategy that buys an equal amount in each stock that has risen in the past day. The Y axis is in candles per second, evaluated as the # of time steps # of assets # of strategies.
